
問題描述
有N個物品, 每個物品Cost為C[i], Value為W[i], 其中 i 屬於 [0, …, N-1]
有一個書包, 容量為V
求書包能裝下的最大Value
為什麼叫0-1背包?
因為每個物品只有2選擇: 不用(0)或者用(1). 物品不能重複使用.
暴力解法
暴力求解就是把N個物品的所有子集(Power Set)求出來, 然後看看所有Cost加起來是不是 <= 背包容量 V, 對滿足以上條件的, 選出最大的Value.
子集一共有2^N個, 所以需要O(2^N)時間.
用DFS(深度優先搜索)的話, 需要O(N)空間
2維DP解法
這是一種背包固定套路, 首先初始化一個2維矩陣dp, N+1行, V+1列.
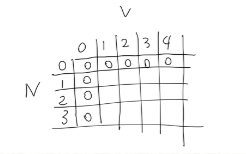
用 Python 表達出來就是
row = [0] * (1 + V)
dp = []
for i in range(N + 1):
dp.append(list(row))dp[i][v] 代表的意義是第0到第i-1個物品 (前i個物品), 容量為v的背包, 能放的最大價值
填格子的時候我們從左到右按行掃描, 也就是對一個特定物品, 第i-1個, 掃描所有可能的容量. 到第i-1個物品的時候, 容量為v的時候, 無非兩種選擇:
1. 把這個物品放進去, 那麼v-C[i]需要大於或等於0, 否則放不下, 新的最大value為 dp[i-1][v-C[i]] + W[i]
2. 不把這個物品放進去. 為什麼不放? 因為放不進了啊. value為 dp[i-1][v]
dp[i][v]需要放這兩種情況中value大的那種. 用python表達就是, 先把dp[i][v]設成不放的情況, 如果可以放的話(v-C[i] >= 0), 並且放了Value增加了, 就換成放的情況. 用Python表達出來就是
for i in range(1, N + 1):
for v in range(1, V + 1):
dp[i][v] = dp[i - 1][v]
if v - C[i] >= 0:
dp[i][v] = max(
dp[i][v],
dp[i - 1][v - C[i - 1]] + W[i - 1]
)注意下標有點tricky. dp[i][v]代表的意義是前i個物品, 所以最後一個物品的index是i-1 (物品下標從0開始). 這就是為什麼要用C[i - 1], W[i - 1]. 很多純理論算法用的是1 base的index, 轉換成code的時候還有點麻煩. 我這裡用的就直接是Python或大部分語言能跑的真code. dp[i][j] 賦值部分就是所謂的DP轉移方程.
最後把初始化, 循環和轉移方程連在一起, 就可以用 Python 完整的表達出來
def maxKnapsackValue(N, C, W, V):
# init dp
row = [0] * (1 + V)
dp = []
for i in range(N + 1):
dp.append(list(row))
for i in range(1, N + 1):
for v in range(1, V + 1):
dp[i][v] = dp[i - 1][v]
if v - C[i - 1] >= 0:
dp[i][v] = max(
dp[i][v],
dp[i - 1][v - C[i - 1]] + W[i - 1]
)
return dp[N][V]以上就是 Python 版本的0-1背包問題的2維DP套路解法
2維DP解法應用
以上總結的2維DP解法的模版可以直接應用在Leetcode 416上, 詳細請看這篇文章.
參考資料
崔添翼 背包問題九講 2.0 原文有些細節講得不清楚, 而且有些偽代碼轉換成真代碼時候有些問題, 本文用能run的真代碼並試圖把細節交代清楚.
