
Here is the question.
I came up with the answer without looking the answer, bottom up dynamic programming (dp) is not a very easy to design at the beginning. Starting from top down + cache, I wrote it a few times, and simplified it a little bit each time, and finally passed the OJ.
Python version.
class Solution(object):
def coinChange(self, coins, amount):
"""
:type coins: List[int]
:type amount: int
:rtype: int
"""
cache = {0:0}
self.dfs(coins, amount, cache)
return cache[amount]
def dfs(self, coins, amount, cache):
if amount in cache:
return cache[amount]
if amount == 0:
return 0
if amount < 0:
return -1
ans = float('inf')
for coin in coins:
rest_cnt = self.dfs(coins, amount - coin, cache)
if rest_cnt != -1:
ans = min(ans, rest_cnt + 1)
if ans == float('inf'):
cache[amount] = -1
return -1
cache[amount] = ans
return ans In order to better understand the algorithm, I added some logs to record how many times dfs was called and cache hits, and the number of times each cache key was written (with cache and without cache).
Use coins = [1, 2, 5] and amount = 11 as an example
With cache
dfs call: 34
cache hit: 15
key write times
1: 1
2: 1
3: 1
4: 1
5: 1
6: 1
7: 1
8: 1
9: 1
10: 1
11: 1without cache
dfs call: 928
cache hit: 0
key write times
1: 128
2: 75
3: 44
4: 26
5: 15
6: 9
7: 5
8: 3
9: 2
10: 1
11: 1The contents of the cache after running are as follows
0: 0
1: 1
2: 1
3: 2
4: 2
5: 1
6: 2
7: 2
8: 3
9: 3
10: 2
11: 3Numbers inside cache are exactly the minimum numbers of coins needed for the target amount from 0 to 11. From this, I think that bottom up dp is exactly what needs to be built for the above cache. dp[0] = 0, the amount is 0, of course, 0 coin is needed to make up a value of 0. dp[amount] depends on whether the value of amount-coin is positive, and whether there is a value other than -1 before. When the amount is being calculated, the previous dp[0] to dp[amount-coin] have been filled in. For all possible coin values, find smallest value of dp[amount – coin], of course, amount - coin needs to be larger or equal to 0 and dp[amount – coin] is not -1, add 1 to it, and you will get dp[amount]. The time complexity is O(amount * len(coins)). The space is O(amount).
class Solution(object):
def coinChange(self, coins, amount):
"""
:type coins: List[int]
:type amount: int
:rtype: int
"""
dp = [0] * (amount + 1)
for i in range(1, amount + 1):
rest_min_cnt = -1
for coin in coins:
rest = i - coin
if rest >= 0 and dp[rest] != -1:
if rest_min_cnt == -1:
rest_min_cnt = dp[rest]
else:
rest_min_cnt = min(rest_min_cnt, dp[rest])
dp[i] = rest_min_cnt + 1 if rest_min_cnt != -1 else -1
return dp[amount] After many days, I tried the Python solution again to see if it has been internalized by me. Compared with the above, some improvements have been made. I used -1 for all dp list initial values, which means it is impossible at the beginning. dp[0] is set to 0, which means that no coin is taken. The new solution get rid of the rest_min_cnt variable above.
class Solution(object):
def coinChange(self, coins, amount):
"""
:type coins: List[int]
:type amount: int
:rtype: int
"""
dp = [-1] * (amount + 1)
dp[0] = 0
for i in range(1, amount + 1):
for j in coins:
k = i - j
if k >= 0 and dp[k] != -1:
if dp[i] == -1:
dp[i] = dp[k] + 1
else:
dp[i] = min(dp[i], dp[k] + 1)
return dp[amount]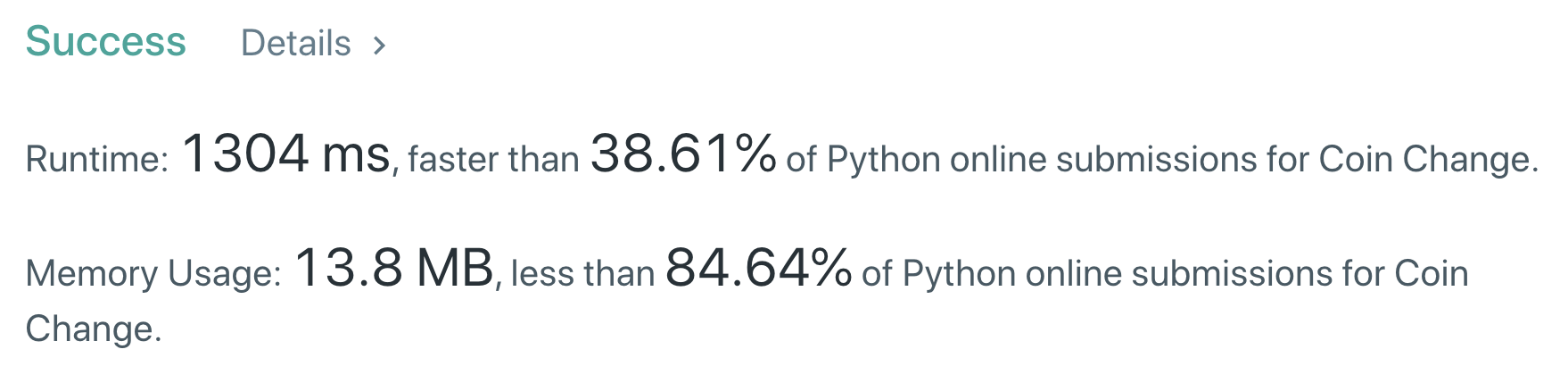
Java version of bottom up dp solution
class Solution {
public int coinChange(int[] coins, int amount) {
int[] dp = new int[amount + 1];
for (int i = 1; i <= amount; i++) {
int restMinCoins = -1;
for (int coin : coins) {
int remainder = i - coin;
if (remainder >= 0 && dp[remainder] != -1) {
if (restMinCoins == -1) {
restMinCoins = dp[remainder];
} else {
restMinCoins = Math.min(restMinCoins, dp[remainder]);
}
}
}
if (restMinCoins == -1) {
dp[i] = -1;
} else {
dp[i] = restMinCoins + 1;
}
}
return dp[amount];
}
}